3軸加速度センサを用いた姿勢推定
はじめに
今回は、加速度センサの値から、ロール・ピッチ・ヨーの回転角を算出してみようと思います。
まずは動画にて、ロール・ピッチ・ヨーの回転に対して、加速度センサの値がどう動くのか、なんとなくイメージをつかんで頂ければと思います。
なんとなく、加速度センサを使って「ロールとピッチの回転角」を検知できそう、というイメージが沸けばOKです。
以下では、動画で直観的に捉えた、ロール・ピッチ・ヨー回転と加速度センサ値との関係について、数学的な観点で考察し、最後に幾何学的な意味に触れます。
解説の流れは次の通り。
----
・計算上必要な「回転行列の特性」について
・加速度センサの特性について
・センサ値からロール・ピッチ回転角の算出
・基準姿勢における座標軸の向き
・幾何学的なイメージ
----
回転行列の特性
最初に、後半の数式の導出において必要となる数学的知識を記載しておきます。
まずは復習。ロール・ピッチ・ヨーの回転角をそれぞれ \(r,p,y\) とした場合、これを表す回転行列 \(R_x(r), R_y(p), R_z(y)\) は、以下のとおり。
R_x(r) = \left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & C_r & -S_r \\
0 & S_r & C_r
\end{array} \right]
,
R_y(p) = \left[
\begin{array}{ccc}
C_p & 0 & S_p \\
0 & 1 & 0 \\
-S_p & 0 & C_p
\end{array} \right]
,
R_z(y) =
\left[ \begin{array}{ccc}
C_y & -S_y & 0 \\
S_y & C_y & 0 \\
0 & 0 & 1
\end{array} \right]
$$
ところでこの回転行列、実は「特殊直行行列」という、ものすごい特性の持ち主です。
この中でも、以降の計算で必要となる「直行行列」の重要な特性を紹介します。
すなわち \( A^{-1} = A^t \)
どうですか!普通、逆行列を求めるのって凄い大変なわけですが、回転行列の場合は転置するだけで逆行列が求まるんです。すごいぜ、回転行列。
加速度センサの特性
加速度センサは、その名の通り「加速度」を検知するセンサです。
そして、地球上にいる限り、静止状態では主に「重力加速度」を検知しています。
検知方向は、反力を検知する作りなので、空を向いたベクトルがセンサ値として出力されます。
この特性に着目し「物体がどんな方向を向いていようとも、重力方向はわかる訳だから、それを基準として今の姿勢を計算してやろう」というのが、加速度センサによる姿勢検知の基本思想になります。
このため、重力加速度以外の加速度がかかっている状態、例えば物体が加減速しながら動いている状況下では、姿勢に誤差が含まれることになります(その誤差が許容できるかどうかは、用途によります)。
M5Stackにおける加速度センサ
M5Stackでは、ディスプレイの裏にMPU9250という9軸センサ(加速度・角速度・方位センサが1つにまとまったもの)が取り付けられています。
センサの仕様書で定義されているセンサ座標軸も併せて表記しました。
今回使用する加速度センサは3軸センサなので、検知された加速度が3次元ベクトル \( ( a_x, a_y, a_z) \) として、センサから出力されることになります。
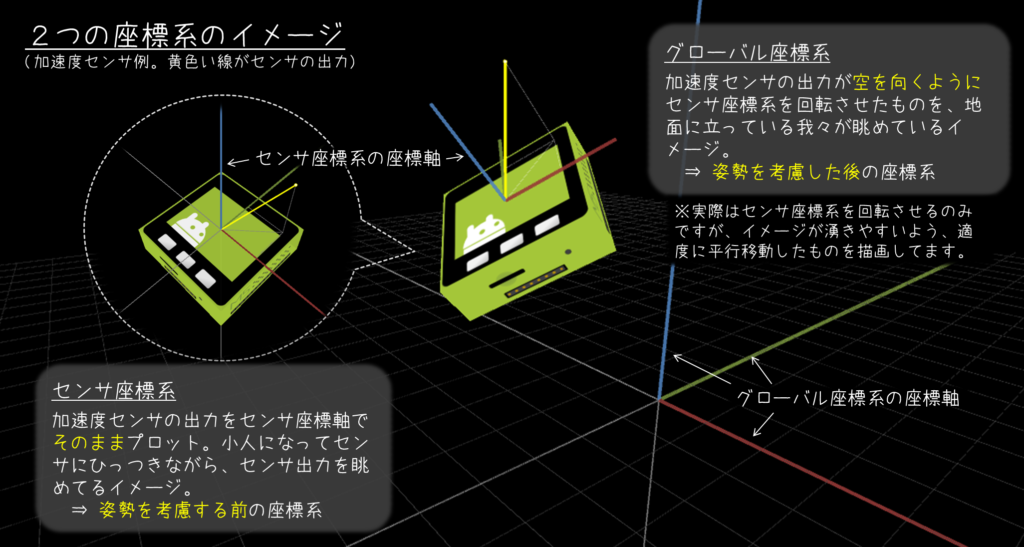
「センサ座標系」と「グローバル座標系」
加速度センサに限らず、センサ全般の話をする際、必ずと言っていいほど「センサ座標系」と「グローバル座標系」という言葉が出てきます。
その違いをまとめてみたイメージ図が以下になります。
つまり、加速度センサの特性に着目し、現在の姿勢を表すための「回転」を求めるためには、次の問題を解けばよいことになります。
少し鶏と卵感がありますが、解きたい問題はこれです。
ちなみに動画では、前半が「センサ座標系」、後半のシミュレートが「グローバル座標系」と対応しています。
加速度センサ値からロール・ピッチ回転角の算出
先ほど設定した問題を、数式で表現してみます。
加速度センサが出力するセンサ座標系のベクトルを \( (a_x, a_y, a_z) \) 、これをグローバル座標系へと回転させるロール・ピッチ・ヨーの回転角を\( r, p, y \) とします。
回転した結果は、グローバル座標系で必ず空を向いているため、重力加速度を\( g \)とすると \( (0, 0, g) \) と表現できます。
これらの各ベクトルを行列とみなすと、回転行列と合わせて次のような数式で表現できます。
R_z(y)R_y(p)R_x(r) \left[ \begin{array}{c} a_x \\ a_y \\ a_z \end{array} \right] = \left[ \begin{array}{c} 0 \\ 0 \\ g \end{array} \right]
$$
両辺に対して逆行列 \(R_z^{-1}(y), R_y^{-1}(p), R_x^{-1}(r)\) を順に左からかけてみます。
\left[ \begin{array}{c} a_x \\ a_y \\ a_z \end{array} \right] = R_x^{-1}(r) R_y^{-1}(p) R_z^{-1}(y)\left[ \begin{array}{c} 0 \\ 0 \\ g \end{array} \right]
$$
ここで、回転行列がもつ直行行列の特性 \( A^{-1} = A^t \)を適用し、展開してみます。
\begin{eqnarray}
\left[ \begin{array}{c} a_x \\ a_y \\ a_z \end{array} \right]
& = &
R_x^t(r) R_y^t(p) R_z^t(y)\left[ \begin{array}{c} 0 \\ 0 \\ g \end{array} \right] \\
& = &
\left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & C_r & S_r\\
0 & -S_r & C_r
\end{array} \right]
\left[
\begin{array}{ccc}
C_p & 0 & -S_p \\
0 & 1 & 0 \\
S_p & 0 & C_p
\end{array} \right]
\left[ \begin{array}{ccc}
C_y & S_y & 0 \\
-S_y & C_y & 0 \\
0 & 0 & 1
\end{array} \right]
\left[ \begin{array}{c} 0 \\ 0 \\ g \end{array} \right] \\
& = &
\left[
\begin{array}{ccc}
C_p & 0 & -S_p \\
S_r S_p & C_r & S_r C_p \\
C_r S_p & -S_r & C_r C_p
\end{array} \right]
\left[ \begin{array}{ccc}
C_y & S_y & 0 \\
-S_y & C_y & 0 \\
0 & 0 & 1
\end{array} \right]
\left[ \begin{array}{c} 0 \\ 0 \\ g \end{array} \right] \\
& = &
\left[ \begin{array}{ccc}
C_p C_y & C_p S_y & -S_p \\
S_r S_p C_y - C_r S_y & S_r S_p S_y + C_r C_y & S_r C_p \\
C_r S_p C_y + S_r S_y & C_r S_p S_y - S_r C_y & C_r C_p
\end{array} \right]
\left[ \begin{array}{c} 0 \\ 0 \\ g \end{array} \right] \\
& = &
\left[ \begin{array}{c}
-S_p g \\
S_r C_p g \\
C_r C_p g
\end{array} \right] \tag{1}
\end{eqnarray}
$$
ここまでで、加速度センサ値 \( (a_x, a_y, a_z) \) とロール・ピッチ・ヨー回転角 \( r, p, y \) の関係を単純な式で表すことができました。
ふとここで式(1)を見てみると、ヨー角 \(y\) が登場していません。
これは、動画で触れた「加速度センサのみでは、ヨー角を算出できなさそう」という現象を表しており、その事実を数学的に示すことができました。
逆に考えれば「ロール角とピッチ角さえ条件を満たせば、ヨー角はなんであろうと、センサ出力は必ず空を向く」という事でもあります。
さて、計算に戻ります。
このままだと重力加速度 \(g\) が邪魔なので、これを消すような工夫をしつつ、ロール・ピッチ回転角 \( r, p \) を算出してみます。
まず、ロール回転角 \( r \) は次の通り。
\begin{eqnarray}
\frac{a_y}{a_z} & = & \frac{S_r C_p g}{C_r C_p g} = \tan r \\
\Leftrightarrow r & = & \arctan \left( \frac{a_y}{a_z} \right)
\end{eqnarray}
$$
次に、ピッチ回転角 \( p \) は次の通り。
\begin{eqnarray}
\frac{a_x}{\sqrt{a_y^2 + a_z^2}} & = & \frac{-S_p g}{\sqrt{(S_r^2 + C_r^2) C_p^2 g^2}} = \frac{-S_p g}{C_p g} = -\tan p \\
\Leftrightarrow p & = & \arctan \left( \frac{-a_x}{\sqrt{a_y^2 + a_z^2}} \right)
\end{eqnarray}
$$
以上の方法により、加速度センサ \( (a_x, a_y, a_z) \) の値から、ロール・ピッチ回転角 \( r, p \) を求めることができました。
ちなみに、数学的には \( \arctan() \) の分母が0だと困っちゃいますが、多くの言語で用意されているatan2()関数は、分母が0のとき (分子>0) ⇒ \( \frac{\pi}{2} \)、(分子<0) ⇒ \( -\frac{\pi}{2} \) を返してくれる作りになっていることが多いので、実質問題にはならないかと思います。
基準姿勢における座標軸の向き
先ほどの計算は、センサ座標系を回転してグローバル座標系へ変換したので、おのずと基準姿勢(=回転前の基準となる姿勢)における座標軸の向きは揃っていました。
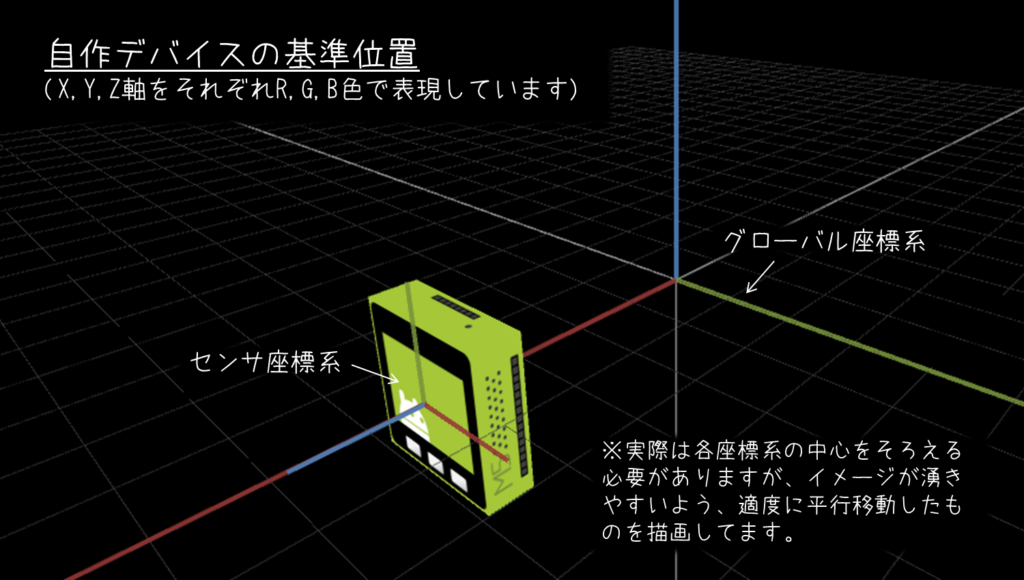
しかし、例えば今回私が制作したデバイスでは、ロール・ピッチ・ヨー回転を直感的にシミュレートできるよう、次のような状態を基準姿勢とする必要がありました。
この状態だと、「グローバル座標系」と「基準姿勢におけるセンサ座標系」の座標軸の向きが揃っていません。
このような場合、軸の向きを揃えるため、前処理としてセンサ出力に変換をかませてやります。
例えば、座標軸の向きが揃っていない状態におけるセンサ出力(いわばM5Stackの「生」のセンサ値)を \( ( a_{x5}, a_{y5}, a_{z5} ) \) 、揃えた後のセンサ出力を \( (a_x, a_y, a_z ) \) とする場合、先ほどの図における軸の対応関係から、今回必要な変換は次の通り。
\left[
\begin{array}{c} a_x \\ a_y \\ a_z
\end{array} \right]
=
\left[
\begin{array}{c} a_{z5} \\ a_{x5} \\ a_{y5}
\end{array} \right]
$$
蓋を開ければ大した話ではないのですが、座標軸の向きを考慮する事はとても重要なので、一応触れておきました。
幾何学的な意味
動画に登場するロール回転角 \( \phi \)、ピッチ回転角 \( \theta \) との対応は、これまでの議論により以下のように表現できます。
\phi = \arctan \left( \frac{a_{x5}}{a_{y5}} \right) \\
\theta = \arctan \left( \frac{-a_{z5}}{\sqrt{a_{x5}^2 + a_{y5}^2}} \right)
$$
これを把握したうえで再度動画を見ると、数式を幾何学的にイメージしやすいかと思います。
なお、もし \( -a_{z5} \) の項について、負の符号を持つことに疑問をもった方は、ピッチ回転の回転方向の定義をもう一度考えてみてください。
また、\( a_{x5}, a_{y5} \) がどちらも 0 の場合、ロール回転角は求まりません。これは幾何学的にはZ軸と完全に重なっている状態で、ピッチ回転角が ±90° の時です。
幾何学的にイメージすると分かりやすいですが、ピッチ回転角が ±90° の時、ロール方向としてどこを向くべきか、決まらないのがわかるかと思います(どこを向いても間違ではない、とも言える)。
このように、ロール・ピッチ・ヨー方式による姿勢の表現には、特異点となる箇所があるので、注意が必要です。
終わりに
今回は、3軸加速度センサの出力から、現在の姿勢を表すロール・ピッチ角を算出してみました。
加速度センサのみでは、原理的にヨー角を算出することはできません。
これは、飛行機の中で紐にくくりつけた5円玉を垂らしたとき、飛行機の傾き具合は分かれど、進んでいる方角はわからないのと同じイメージです。
ここで、例えば方位センサと組み合わせることで、ヨー角も算出することができます。
次回は、この辺りの話を記事にしてみたいと思っています。
ということで、また次回をお楽しみに。