3軸方位センサを用いた姿勢推定
はじめに
前回は、加速度センサの値から、ロール・ピッチ回転角を算出してみました。
今回は、これに方位センサを加え、新たに「ヨー回転角」を算出してみようと思います。
まずは動画にて、方位センサの値がどのような特性をもっているのか、なんとなくイメージをつかんで頂ければと思います。
以下では、動画の中で出てきた内容について解説しつつ、数学的な観点で考察してみようと思います。
解説の流れは次の通り。
----
・方位センサの特性について
・オフセット補正
・センサ値からヨー回転角の算出
・基準姿勢における座標軸の向き
・幾何学的考察による計算量の削減
----
方位センサの特性について
多くの方は、理科の実験などで「方位磁石」に触れたことがあると思います。
このイメージ通り、方位センサは「北」を検知するセンサです。
「センサの向いている方角がわかれば、ヨー角が算出できそう!」というのは、前回までの議論で、直観的にイメージしやすいかと思います。
基本イメージはそれでいいのですが、3軸方位センサ特有の注意すべき特性があるので、まずはそれらについて触れたいと思います。
特性1.オフセットの存在
3軸方位センサは地磁気を検知し、「北」を示す \( (d_x, d_y, d_z)\) のような3次元ベクトルを出力します。
(正確には「北極点」と「地磁気が示す北」の間には「偏角」というズレが存在しますが、今回の目的は正確な北を算出する事ではないので、ここでは考慮しません)
動画前半で登場しましたが、出力されたセンサ値を単純にプロットすると、センサ座標系の中心からほど遠い場所で球体が描かれます。
これは、方位センサに「オフセット」が乗っているためです。
オフセットが乗る理由は様々で、センサ固有の特性や緯度・経度、周囲の磁場の状況など、色んな要因があります。
そこで、北を知るためには、まず球体の中心を算出し、座標系の中心に持ってくる必要があります。これを「オフセット補正」と呼びます。
スマホなどで地図アプリを使っている時、たまに「スマホをぐるぐる回してください」と表示されるのは、この球体の中心を求めるためです。
特性2.姿勢推定の必要性
昔、理科の実験で使った「方位磁石」は、大雑把に言うと「机の上で使うこと」を前提に作られています。例えば、部屋の壁に貼り付けて使おうとしても、北を指すことはできません。
これはある意味、方位磁石は2軸方位センサ(=2次元の平面方向のみ検知)であると言えます。
これに対し、3軸方位センサを使う場合、壁に貼り付けようがなんだろうが、3次元ベクトルで北を教えてくれるので、どんな向きで置いてもかまいません。
その代わり、机の上に置かれるという前提がない分、センサがどんな傾きで置かれているのかを検知(=姿勢推定)し、出力される3次元ベクトルの意味を解釈してやる必要が出てきます。
幸いにも、今回使っている9軸センサMPU9250には「加速度センサ」が一緒についているため、これを使ってセンサの傾きを知ることができます。
このため、今回は加速度センサを併用することで、方位センサの姿勢を推定し、北を検知することになります。
オフセット補正
ここでは「特性1.オフセットの存在」で解説した、オフセット補正の方法について述べます。
具体的な手法の詳細は、こちらのスライド(作: ロケット小僧 様)が超絶分かりやすいです。ご一読いただくことをオススメします。
最小二乗法による球面近似
まず、ぐるぐる色んな方向にセンサを回し、球体っぽいセンサ値が取得できたとします。
今、球体の中心を知りたいので、ある中心と半径をもつ「球面の関数」で近似することを考えます。
最も理想的な近似は「全てのセンサ値が、近似した球面上にあること」ですが、各センサ値はノイズを含んでいるため、そんなうまくはいきません。
なので、せめて各センサ値と球面の誤差が小さくなるよう、中心と半径を求めてやります。
このように
----
・近似したい関数が分かっている(=今回は球面)
・既に取得した全ての点との誤差が小さくなるような近似をしたい
----
という時に、便利な手法のひとつが最小二乗法です。
上記サイト様より、今回のケースに最小二乗法を適用して最終的に導出される式は、以下の通りです。
(ただし、後のガウス消去法で効率よく解くため、表記の順番を変えています)
\left[ \begin{array}{cccc}
\Sigma x_i & \Sigma x_i^2 & \Sigma x_i y_i & \Sigma x_i z_i \\
\Sigma y_i & \Sigma x_i y_i & \Sigma y_i^2 & \Sigma y_i z_i \\
\Sigma z_i & \Sigma x_i z_i & \Sigma y_i z_i & \Sigma z_i^2 \\
\Sigma 1 & \Sigma x_i & \Sigma y_i & \Sigma z_i
\end{array} \right]
\left[ \begin{array}{c}
c_x^2+c_y^2+c_z^2-r^2 \\ -2c_x \\ -2c_y \\ -2c_z
\end{array} \right]
=
\left[ \begin{array}{cccc}
- \Sigma x_i (x_i^2 + y_i^2 + z_i^2) \\
- \Sigma y_i (x_i^2 + y_i^2 + z_i^2) \\
- \Sigma z_i (x_i^2 + y_i^2 + z_i^2) \\
- \Sigma (x_i^2 + y_i^2 + z_i^2)
\end{array} \right]
$$
今一度確認ですが、今回求めたいのはオフセット量、つまり近似した球面の中心 \( ( c_x, c_y, c_z ) \) です。
上記のような「連立1次方程式が行列で表現されたもの」をコンピュータで効率よく解くための手法として「ガウスの消去法」があります。
詳細はググッて頂くとして、前進消去により、下段から順に答えが算出されます( \( c_z⇒c_y⇒c_x \) の順 )。
今回は半径 \( r \) を算出する必要はないため、引用元の式とは順番を入れ替えることで、計算量を少し減らしてみました(大した削減にはならないかもしれませんが…)。
以上の方法により、オフセット量を算出することができます。
方位センサ値からヨー回転角の算出
次に「特性2.姿勢推定の必要性」で触れた、加速度センサによる姿勢推定の原理について解説します。
特性2.で述べた通り、方位センサの値をオフセット補正しただけでは、センサ自体がどんな向きで置かれているのかがわからないため、「ヨー角」を算出することができません。
しかし我々は幸いにも「加速度センサの出力が必ず空を向く(=必ず地面と水平になる)回転」を算出する術について、前回の記事で学びました。
そこで、今回も加速度センサから得たロール・ピッチ回転を適用することで、どんな姿勢であってもセンサを机の上に置いた(=地面と水平な)状態相当となるよう、方位センサの出力を補正(=回転)してやります。
ところで動画にて、方位センサの出力にロール・ピッチ回転を適用した後の状態も示していますが、XY平面に平行ではなく、少し下を向いた方向が検知されているのがわかります。
実はこれで正しくて、現在の日本では、地磁気による北は地面へ刺さる向きに検知されます。このため日本の方位磁石の針は、地面と水平になるよう、S極側が少し重く作られているそうですよ。へぇ~。
(この辺りの地磁気の詳しい話は、こちらの気象庁地磁気観測所の説明がわかりやすいです)
方位磁石がS極側を少し重くしているのと同様、最終的に地面に刺さる方向の成分は無視して、あくまで地面に水平なベクトル成分のみから、ヨー角を算出することにします。
以上の議論から、ヨー角を算出するためには、次の問題を解くことになります。
では、設定した問題を解いてみます。
センサ座標系における、オフセット補正された方位センサからの出力を \( (d_x, d_y, d_z) \) 、これをグローバル座標系へと回転させる、加速度センサから算出したロール・ピッチの回転角を\( r, p \) とします。
また、グローバル座標系における回転後の結果を \( (D_x, D_y, D_z) \) とすると、各ベクトルを行列とみなしたとき、回転行列と合わせて次のような数式で表現できます。
R_y(p)R_x(r) \left[ \begin{array}{c} d_x \\ d_y \\ d_z \end{array} \right]
=
\left[ \begin{array}{c} D_x \\ D_y \\ D_z \end{array} \right]
$$
順次、展開します。
\begin{eqnarray}
\left[ \begin{array}{c} D_x \\ D_y \\ D_z \end{array} \right]
& = &
R_y(p)R_x(r) \left[ \begin{array}{c} d_x \\ d_y \\ d_z \end{array} \right] \\
& = &
\left[\begin{array}{ccc}
C_p & 0 & S_p \\
0 & 1 & 0 \\
-S_p & 0 & C_p
\end{array} \right]
\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & C_r & -S_r \\
0 & S_r & C_r
\end{array} \right]
\left[ \begin{array}{c} d_x \\ d_y \\ d_z \end{array} \right] \\
& = &
\left[\begin{array}{ccc}
C_p & S_p S_r & S_p C_r \\
0 & C_r & -S_r \\
-S_p & C_p S_r & C_p C_r
\end{array} \right]
\left[ \begin{array}{c} d_x \\ d_y \\ d_z \end{array} \right] \\
& = &
\left[ \begin{array}{c}
C_p d_x + S_p S_r d_y + S_p C_r d_z \\
C_r d_y - S_r d_z \\
-S_p d_x + C_p S_r d_y + C_p C_r d_z \\
\end{array} \right] \\
\end{eqnarray}
$$
ここで再度確認ですが、回転後のベクトル\( ( D_x, D_y, D_z ) \) は、地面と水平にセンサを置いたときの出力に相当します(=動画中盤において、軌跡が地面と水平な円を描く、M5Stackから伸びた黄色いベクトル)。
「北」を指して、地面へ刺さる方向のベクトルとなっているため、\( D_z \) 成分を無視し、\( D_x, D_y \)成分のみからヨー角を算出します。
また、回転方向に着目して動画を見ると、センサの乗ったM5Stackを「反時計回り」に回転させた場合、センサ出力を示す黄色いベクトルは「時計回り」に回転しています。
つまり、回転方向が逆の関係にあります(よくよく考えればあたり前ですが)。
以上より、「北」を0°としたヨー角 \( y \) と、\( D_x, D_y \)の関係は、以下のように表すことができます。
\begin{eqnarray}
\tan y & = & - \frac{D_y}{D_x} \\
\Leftrightarrow y & = & \arctan \left( -\frac{D_y}{D_x} \right) \\
& = &
\arctan \left( - \frac{C_r d_y - S_r d_z}{C_p d_x + S_p S_r d_y + S_p C_r d_z} \right) \tag{1}
\end{eqnarray}
$$
以上の方法により、ヨー回転角 \( y \) を求めることができました。
基準姿勢における座標軸の向き
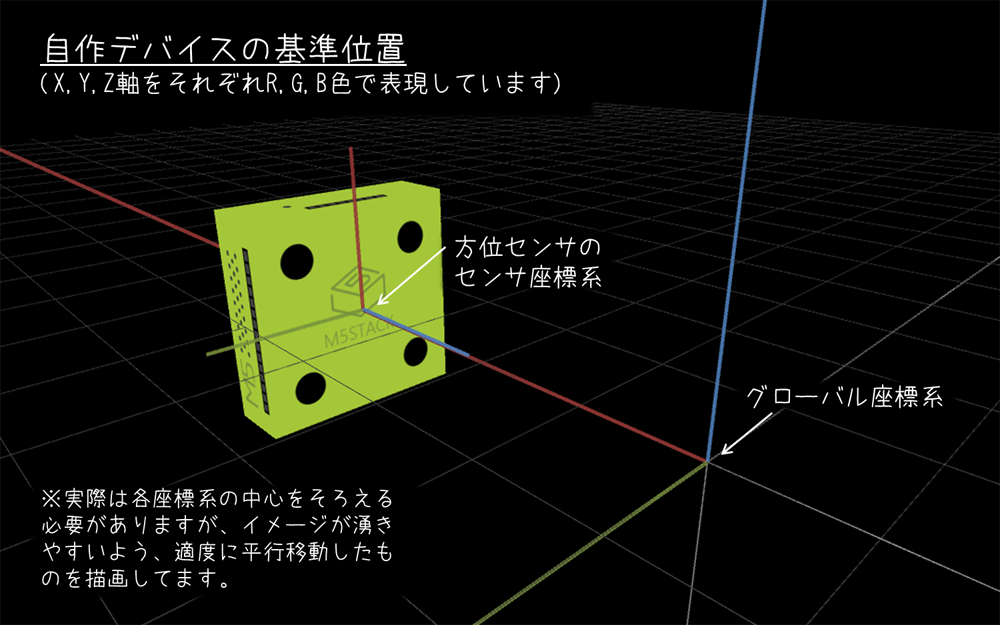
前回の加速度センサの時と同様、自作デバイスでは「グローバル座標系」と「基準姿勢におけるセンサ座標系」の座標軸の向きが揃っていないため、以下のような変換をかませてやります。
座標軸の向きが揃っていない状態における方位センサの出力(いわばM5Stackの「生」のセンサ値)を \( (d_{x5},d_{y5},d_{z5}) \)、揃えた後のセンサ出力を \( (d_x,d_y,d_z) \) とする場合、先ほどの図における軸の対応関係から、今回必要な変換は次の通り。
\left[
\begin{array}{c} d_x \\ d_y \\ d_z
\end{array} \right]
=
\left[
\begin{array}{c} -d_{z5} \\ d_{y5} \\ d_{x5}
\end{array} \right] \tag{2}
$$
幾何学的考察による計算量の削減
動画に登場するヨー回転角 \( \psi \)は、式(1)、(2)より以下のように表現できます。
\psi = \arctan \left( - \frac{C_r d_{y5} - S_r d_{x5}}{ -C_p d_{z5} + S_p S_r d_{y5} + S_p C_r d_{x5}} \right) \tag{3}
$$
このまま、加速度センサから算出済みのロール・ピッチ回転角を使って三角関数を適用してもいいのですが、三角関数は処理が重いイメージがあるので、なるべく避けたいところ。
そこで前回の記事より、ロール・ピッチ回転角と加速度センサの値の関係を幾何学的に考えてみると、以下のように表すことができます。
\begin{eqnarray}
C_r & = & \frac{a_{y5}}{\sqrt{a_{x5}^2 + a_{y5}^2}} ~ S_r = \frac{a_{x5}}{\sqrt{a_{x5}^2 + a_{y5}^2}} \\
C_p & = & \frac{\sqrt{a_{x5}^2 + a_{y5}^2}}{\sqrt{a_{x5}^2 + a_{y5}^2 + a_{z5}^2}} S_p = \frac{-a_{z5}}{\sqrt{a_{x5}^2 + a_{y5}^2 + a_{z5}^2}} \\
\end{eqnarray}
$$
※ピッチの回転方向の定義から、\( S_p \) が負の符号を持つことに注意。
これらを式(3)に代入し、分子・分母に \( \sqrt{a_{x5}^2 + a_{y5}^2}, \sqrt{a_{x5}^2 + a_{y5}^2 + a_{z5}^2} \) を掛けて整理すると
\begin{eqnarray}
\psi & = & \arctan \left( - \frac{ ( a_{y5}d_{y5} - a_{x5}d_{x5} ) \sqrt{a_{x5}^2 + a_{y5}^2 + a_{z5}^2} }{ -(a_{x5}^2 + a_{y5}^2) d_{z5} - a_{z5}( a_{x5}d_{y5} + a_{y5} d_{x5} ) } \right) \\
& = &
\arctan \left( \frac{ ( a_{x5}d_{x5} - a_{y5}d_{y5} ) \sqrt{A + a_{z5}^2} }{ A d_{z5} + a_{z5}( a_{x5}d_{y5} + a_{y5}d_{x5} ) } \right) ( ただしA = a_{x5}^2 + a_{y5}^2 ) \tag{4}
\end{eqnarray}
$$
計算量の比較
式(1), (4)共に、\( \arctan \)、除算1回は共通なので、それ以外の演算回数を比較してみます。
----
【式(1)】 加減算: 3, 乗算: 7, 三角関数: 4
【式(4)】 加減算: 5, 乗算: 9, 平方根: 1
----
M5Stackに乗っているマイコンESP32には、浮動小数点の乗算ユニットが載っているので、式(4)のほうが速いのかな?でも、三角関数の近似の真面目具合によっては式(1)のほうが速いかもしれぬ…。また、計算精度はどうなんだろう。余裕があったら、今度測定してみようと思います。
おわりに
今回は、方位センサを用いたヨー角の算出方法についてまとめてみました。
前回の加速度センサと合わせ、ついにロール・ピッチ・ヨー回転角による姿勢表現が完成しました。
ただ、これらのセンサは安定性も考慮した場合、「高周波な(=細かい)動作の検知が苦手」という傾向にあります。
また、加速度センサは「静止状態以外での検知」が苦手、磁気センサは「地磁気以外の磁気がある環境」が苦手、といった弱点もあります。
そこで、これらの弱点を補う手段として「角速度センサ」にスポットライトがあたります。もちろん、このセンサにも弱点はあるのですが…。
次回は、この「角速度センサ」を用いた姿勢推定について、記載してみようと思います。
では、また次回をお楽しみに。