3軸角速度センサによる姿勢推定
はじめに
今回は、角速度センサを使った姿勢推定について、解説したいと思います。
前回までの加速度・方位センサに比べて、角速度センサは「高周波な(=細かい)動きの検知」が得意なセンサとなっています。
今回は数式がたくさん出てくる、なかなかな大作となっています。嫌ですね~、でも頑張りましょう。
まずは動画にて、角速度センサがどのような特性をもっているのか、なんとなくイメージをつかんで頂ければと思います。
以下では、動画の中で出てきた内容に触れつつ、数学的な観点で考察してみようと思います。
解説の流れは次の通り。
----
・角速度センサの特性について
・問題の数式化とその意味
・「微小」を生かした式の変形
・最後の仕上げ(変換式の導出)
・基準姿勢における座標軸の向き
・角速度センサの弱点
----
角速度センサの特性について
今までのセンサとの違い
これまで、3軸加速度センサや方位センサの値から、姿勢推定としてロール・ピッチ・ヨーの回転角を算出してきました。
これらのセンサから出力される情報は、重力加速度や地磁気の「向きとその強さ」を表しており、3次元ベクトルとして考えることができました。
今回の角速度センサの出力も \( ( w_x, w_y, w_z ) \) のような3次元の情報であり、一見今までと同じように見えます。
しかし、今回は若干毛色が異なり、その中身は「ある瞬間の回転に対して、 \( x, y, z \) の各軸で検知した角速度」を意味しています。
角速度とは、大雑把にいうと「回転の速度を、1秒間に回転する角度で表したもの」です。
このため「角速度 × 時間 = 回転角(その時間に回転した角度)」を意味します。
今回の姿勢推定では、角速度を直接扱うのではなく、回転角を算出し、それを用いて計算することになります。
このため、正式に以下のような定義をしておきます。
( \delta \phi,\ \delta \theta,\ \delta \psi ) = ( w_x \delta t,\ w_y \delta t,\ w_z \delta t )
$$
※「微小時間」なんて小難しく書きましたが、 \( \delta t \) とは実質「前回のセンサ値取得から、今回取得するまでの経過時間」です。また、\( \delta t \)を十分に短く取れない場合精度が落ちますが、時間積分の方法を工夫する事で多少改善できます。(例えば、台形近似してみる等)
さて、ここまでの議論を振り返ると、角速度センサで検知できるのは「前回の姿勢から \( \delta t \) の間に回転した角度」ということになります。
今まで扱ってきた加速度センサや方位センサとの決定的な違いはここで、角速度センサを用いる場合、必ず「前回の姿勢」が必要になります。
そして、これに「センサから取得した最新の回転角」を足すことで、姿勢を最新の状態に更新していくイメージになります。
よく、角速度センサは「誤差が累積されてしまう」という話を聞きますが、そのデメリットはここに起因しているわけですね。
回転角の性質の違い
ここまでの議論で、姿勢推定をするためには「前回の姿勢」に「最新の回転角」を足しこむ必要があることが分かりました。
これをもう少し掘り下げてみます。
まず「前回の姿勢」について、我々は「ロール・ピッチ・ヨーの回転角」により表現しています。
一方「最新の回転角」は、角速度センサ出力から算出される「\( \delta t \) の間における \( x, y, z \) の各軸の回転角」になります。
この2つの回転角、どちらも \( x, y, z \) 軸周りの回転を表しており、一見同じように見えます。しかし、実は決定的な性質の違いがあります。それは
「回転順を無視できるか、否か」
です。
「…何言ってんだコイツ」という、モヤっとした気持ちが生まれたかもしれません。
そんな方は、こちらの「無限小回転1」「無限小回転2」(物理のかぎしっぽ様) をご一読いただくことをお勧めします。
説明がとても丁寧で分かりやすく、筆者の思いが伝わってくる文章も素敵で、とてもありがたいです。
さて、上記ブログ様の用語をお借りすると、以下のようになります。
----
・「前回の姿勢」は有限回転であり、回転の順番で結果が変わる。
⇒ 順番を考慮した上で足しこむ必要あり。(面倒だなぁ)
・「最新の回転角」は微小回転であり、回転の順番は無視できる。
⇒ 順番を考慮せず、そのまま使える。(こりゃ楽ちん)
----
以上より、「前回の姿勢」のほうだけ回転順をケアする必要があります。
具体的には、回転角を足しこむ前に、「最新の回転角」に対して「前回の姿勢(=ロール・ピッチ・ヨー)」の回転の順番を考慮した変換を施す必要があります。
これらを後ほど数式で表現するため、先ほどのブログ様より重要な要素を抜粋しておきます。
A = E + \varepsilon, ただし \varepsilon =
\left[ \begin{array}{ccc}
0 & -\delta \psi & \delta \theta \\
\delta \psi & 0 & -\delta \phi \\
-\delta \theta & \delta \phi & 0
\end{array} \right]
$$
さて、ここまでの議論で、今回解きたい問題がだいぶ固まりました。まとめると、次のようになります。
ちなみに、回転行列の復習。ロール・ピッチ・ヨーの回転角をそれぞれ \(r,p,y\) とした場合、各 \( x, y, z \) 軸周りの回転を表す回転行列 \(R_x(r), R_y(p), R_z(y)\) は、以下のとおり。
R_x(r) = \left[
\begin{array}{ccc}
1 & 0 & 0 \\
0 & C_r & -S_r \\
0 & S_r & C_r
\end{array} \right]
,
R_y(p) = \left[
\begin{array}{ccc}
C_p & 0 & S_p \\
0 & 1 & 0 \\
-S_p & 0 & C_p
\end{array} \right]
,
R_z(y) =
\left[ \begin{array}{ccc}
C_y & -S_y & 0 \\
S_y & C_y & 0 \\
0 & 0 & 0
\end{array} \right]
$$
問題の数式化とその意味
さて、先ほど設定した問題を解くにあたって、先に \( ( \delta r,\ \delta p,\ \delta y ) \) と \( ( \delta \phi,\ \delta \theta,\ \delta \psi ) \) の関係を表す式を提示します。
R_z(y+\delta y) R_y(p+\delta p) R_x(r+\delta r) = R_z(y) R_y(p) R_x(r) (E + \varepsilon) \tag{1} \\[10pt]
ただし \varepsilon =
\left[ \begin{array}{ccc}
0 & -\delta \psi & \delta \theta \\
\delta \psi & 0 & -\delta \phi \\
-\delta \theta & \delta \phi & 0
\end{array} \right]
$$
左辺と右辺は見方が違うだけで、共に「現在の姿勢を表す回転行列」を意味しています。
以下に、左辺と右辺の考え方を示します。ポイントは「前回姿勢からの微小回転をどう表現するか」の違いです。
⇒ 前回の姿勢を表すロール・ピッチ・ヨー回転角をそれぞれ \( ( r, p, y ) \) 、そこから \( \delta t \) の間に微小回転したロール・ピッチ・ヨー回転角相当を \( ( \delta r, \delta p, \delta y ) \) として、現在の姿勢を表現。
【右辺】微小回転を \( ( \delta \phi,\ \delta \theta,\ \delta \psi ) \) で表現。
⇒ センサ座標系において、\( \delta t \) の間に角速度センサで検知した各 \( x, y, z \) 軸周りの微小回転を \( ( \delta \phi, \delta \theta, \delta \psi ) \) として最新の回転を適用したのち、前回のロール・ピッチ・ヨー回転を適用することで、現在の姿勢を表現。
再確認ですが、今やりたいことは \( ( \delta r,\ \delta p,\ \delta y ) \) を \( ( \delta \phi,\ \delta \theta,\ \delta \psi ) \) で表現する事です。
これができれば、センサの出力から \( ( \delta r, \delta p, \delta y ) \) を算出し、それを前回のロール・ピッチ・ヨー回転角に足しこむことで、現在の姿勢へと更新することができます。
ここまで理解できれば、残るは式(1) をひたすら解くだけです。
「微小」を生かした式の変形
さて、式(1)を解きたいのですが、こやつ、なかなかに複雑な形をしているため、丸腰で挑むには少々勝ち目が薄いです。
でも安心してください。我々は今、\( \delta \) が付いている変数は全て「微小な」回転という前提に立っているので、普段は使えない多くの技を駆使することができます。
これを使って、式(1)を整理してみます。
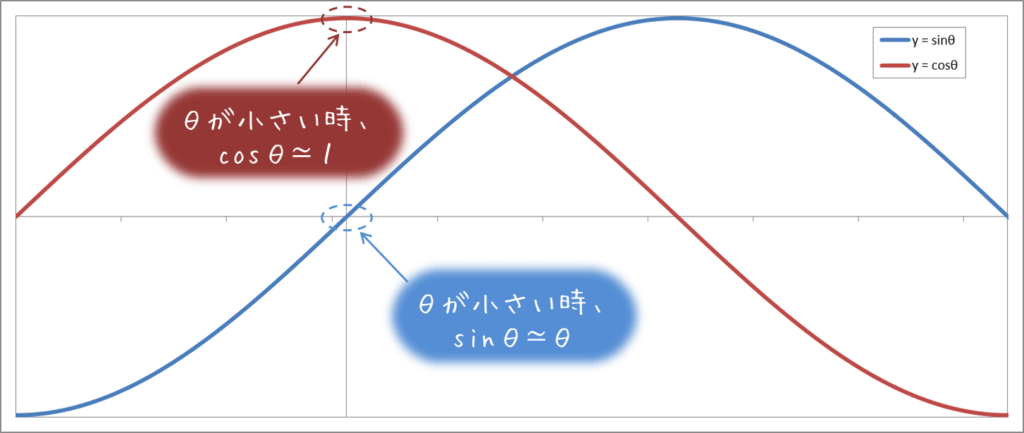
技1: sin, cosの近似
詳しい証明は省略しますが、直感的なイメージとしては以下の図の通り。
この技を使うと、式(1)の左辺の展開が大分楽になります。
例えば、左辺の \( R_x( r + \delta r ) \) を加法定理で展開してみます。
\begin{eqnarray}
R_x(r + \delta r)
& = & \left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & C_{r+\delta r} & -S_{r+\delta r} \\
0 & S_{r+\delta r} & C_{r+\delta r}
\end{array} \right] \\
& = & \left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & C_r C_{\delta r} - S_r S_{\delta r} & -S_r C_{\delta r} - C_r S_{\delta r} \\
0 & S_r C_{\delta r} + C_r S_{\delta r} & C_r C_{\delta r} - S_r S_{\delta r}
\end{array} \right] \tag{2}
\end{eqnarray}
$$
ここで、\( S_{\delta r} \simeq \delta r, C_{\delta r} \simeq 1 \) であることから
\begin{eqnarray}
式(2)
& = & \left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & C_r - \delta r S_r & -S_r - \delta r C_r \\
0 & S_r + \delta r C_r & C_r - \delta r S_r
\end{array} \right] \\
& = & R_x( r ) + \delta r T_x( r ) ただし、T_x(r) = \left[\begin{array}{ccc}
0 & 0 & 0 \\
0 & -S_r & -C_r \\
0 & C_r & -S_r
\end{array} \right]
\end{eqnarray}
$$
同様に
R_y(p + \delta p) = R_y( p ) + \delta p T_y( p ) ただし、T_y(p) = \left[\begin{array}{ccc}
-S_p & 0 & C_p \\
0 & 0 & 0 \\
-C_p & 0 & -S_p
\end{array} \right]
$$
R_z(y + \delta y) = R_z( y ) + \delta y T_z( y ) ただし、T_z(y) = \left[\begin{array}{ccc}
-S_y & -C_y & 0 \\
C_y & -S_y & 0 \\
0 & 0 & 0
\end{array} \right]
$$
以上より、式(1)の左辺は以下のように書き直すことができます。
式(1)の左辺 = (R_z(y)+ \delta y T_z(y))(R_y(p)+ \delta p T_y(p))(R_x(r)+ \delta r T_x(r)) \tag{2}
$$
技2: (微小)x(微小)=0
微小なもの同士の掛け算については、0とみなして無視します。
この技を使うことで、式(2)の展開が大分楽になります。展開した結果を以下に示します。
R_z(y)R_y(p)R_x(r) + \delta y T_z(y)R_y(p)R_x(r) + \delta p R_z(y)T_y(p)R_x(r) + \delta r R_z(y)R_y(p)T_x(r) \\[10pt]
$$
さて、この式は元を辿ると式(1)の左辺なわけですが、今や \( R_z(y) R_y(p) R_x(r) \) という項が存在しています。
そこで、式(1)の右辺をよくよく確認してみると…、いますね!展開したら同様に出てきます。
ということで、両辺から消し去って、最終的に式(1)は以下のように整理できます。
\delta y T_z(y)R_y(p)R_x(r) + \delta p R_z(y)T_y(p)R_x(r) + \delta r R_z(y)R_y(p)T_x(r) = R_z(y) R_y(p) R_x(r) \varepsilon \\[10pt]
$$
さらに計算量を減らすため、左から \( R_z^{-1}(y) \) を掛けて、以下のような形にします。
\delta y R_z^t(y)T_z(y)R_y(p)R_x(r) + \delta p T_y(p)R_x(r) + \delta r R_y(p)T_x(r) = R_y(p) R_x(r) \varepsilon \tag{3} \\[10pt]
$$
左辺の第1項については計算が増えてますが、これは後の計算で綺麗になります。
なお復習ですが、回転行列の特性より \( R_z^{-1}(y) \) は \( R_z^t(y) \) として表記しています。
ふー、大分整理できたぜ。
最後の仕上げ(変換式の導出)
あとは、これまでに定義してきた変数を式(3)に代入し、解くだけです。
ここで種明かし。式(3)の第1項の行列計算は、前からやると実に楽ちん。
\begin{eqnarray}
式(3)の第1項 & = & \delta y R_z^t(y)T_z(y)R_y(p)R_x(r) \\[10pt]
& = & \delta y
\left[\begin{array}{ccc}
C_y & S_y & 0 \\
-S_y & C_y & 0 \\
0 & 0 & 1
\end{array} \right]
\left[\begin{array}{ccc}
-S_y & -C_y & 0 \\
C_y & -S_y & 0 \\
0 & 0 & 0
\end{array} \right]
R_y(p)R_x(r) \\
& = & \delta y
\left[\begin{array}{ccc}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 0
\end{array} \right]
\left[\begin{array}{ccc}
C_p & 0 & S_p \\
0 & 1 & 0 \\
-S_p & 0 & C_p
\end{array} \right]
R_x(r) \\
& = & \delta y
\left[\begin{array}{ccc}
0 & -1 & 0 \\
C_p & 0 & S_p \\
0 & 0 & 0
\end{array} \right]
\left[\begin{array}{ccc}
1 & 0 & 0 \\
0 & C_r & -S_r \\
0 & S_r & C_r
\end{array} \right] \\
& = & \delta y
\left[\begin{array}{ccc}
0 & -C_r & S_r \\
C_p & S_p S_r & S_p C_r \\
0 & 0 & 0
\end{array} \right] \\[10pt]
\end{eqnarray}
$$
これ、凄くないですか。行列を4つもかけてるのに、結果がこんなにシンプル。これを発見したときは思わず「うおー!キタ~!」と唸りました。
そして、他の項も計算して式(3)に代入すると、以下のような式が完成します。
\delta y
\left[\begin{array}{ccc}
0 & -C_r & S_r \\
C_p & S_p S_r & S_p C_r \\
0 & 0 & 0
\end{array} \right]
+ \delta p
\left[\begin{array}{ccc}
-S_p & C_p S_r & C_p C_r \\
0 & 0 & 0 \\
-C_p & -S_p S_r & -S_p C_r
\end{array} \right]
+ \delta r
\left[\begin{array}{ccc}
0 & S_p C_r & -S_p S_r \\
0 & -S_r & -C_r \\
0 & C_p C_r & -C_p S_r
\end{array} \right] \\
=
\left[\begin{array}{ccc}
S_p S_r \delta\psi - S_p C_r \delta\theta & -C_p \delta\psi + S_p C_r \delta\phi & C_p \delta\theta - S_p S_r \delta\phi \\
C_r \delta\psi + S_r \delta\theta & -S_r \delta\phi & -C_r \delta\phi \\
C_p S_r \delta\psi - C_p C_r \delta\theta & S_p \delta\psi + C_p C_r \delta\phi & -S_p \delta\theta - C_p S_r \delta\phi
\end{array} \right]\\[10pt]
$$
ぱっと見凄いことになってますが、ある要素だけ着目すれば、この式は簡単に解けます。
まず、2行1列目の要素を抜き出すと、\( \delta y \) が求まります。
\begin{eqnarray}
\delta y C_p & = & C_r \delta \psi + S_r \delta \theta \\[10pt]
\Leftrightarrow \delta y
& = &
\frac{S_r}{C_p} \delta \theta + \frac{C_r}{C_p} \delta \psi \tag{4}
\end{eqnarray}\\[10pt]
$$
次に、3行1列目の要素を抜き出すと、\( \delta p \) が求まります。
\begin{eqnarray}
-\delta p C_p & = & C_p S_r \delta \psi - C_p C_r \delta \theta \\[10pt]
\Leftrightarrow \delta p
& = &
C_r \delta \theta - S_r \delta \psi \tag{5}
\end{eqnarray}\\[10pt]
$$
最後に、2行2列目の要素を抜き出すと、\( \delta r \) が求まります。
\begin{eqnarray}
-\delta y S_p S_r - \delta r S_r & = & -S_r \delta \phi \\[10pt]
\Leftrightarrow \delta r
& = &
\delta \phi + \delta y S_p = \delta \phi + S_r \frac{S_p}{C_p} \delta \theta + C_r \frac{S_p}{C_p} \delta \psi \tag{6}
\end{eqnarray}\\[10pt]
$$
今回は計算が楽そうな要素を選びましたが、他のどの要素から算出しても、上記の結果を得ることができます。
さて、以上の式(4)~(6)を一つにまとめると、最終的に以下のような結果が得られます。
\left[ \begin{array}{c}
\delta r \\
\delta p \\
\delta y
\end{array} \right]
=
\left[ \begin{array}{ccc}
1 & S_r \frac{S_p}{C_p} & C_r \frac{S_p}{C_p} \\
0 & C_r & -S_r \\
0 & S_r \frac{1}{C_p} & C_r \frac{1}{C_p} \\
\end{array} \right]
\left[ \begin{array}{c}
\delta \phi \\
\delta \theta \\
\delta \psi
\end{array} \right] \\[10pt] \tag{7}
$$
おー!当初の目的であった「センサ出力から算出した回転角 \( ( \delta \phi,\ \delta \theta,\ \delta \psi ) \) を使って、ロール・ピッチ・ヨー回転角 \( ( \delta r,\ \delta p,\ \delta y ) \) を表現」することができました!ひゃっほう、やったぜ!(歓喜の舞)
ということで、この変換式(7)を使うことで、センサ出力からロール・ピッチ・ヨー回転角相当を算出し、前回の姿勢に足しこむことで、最新の姿勢へと更新することができます。
基準姿勢における座標軸の向き
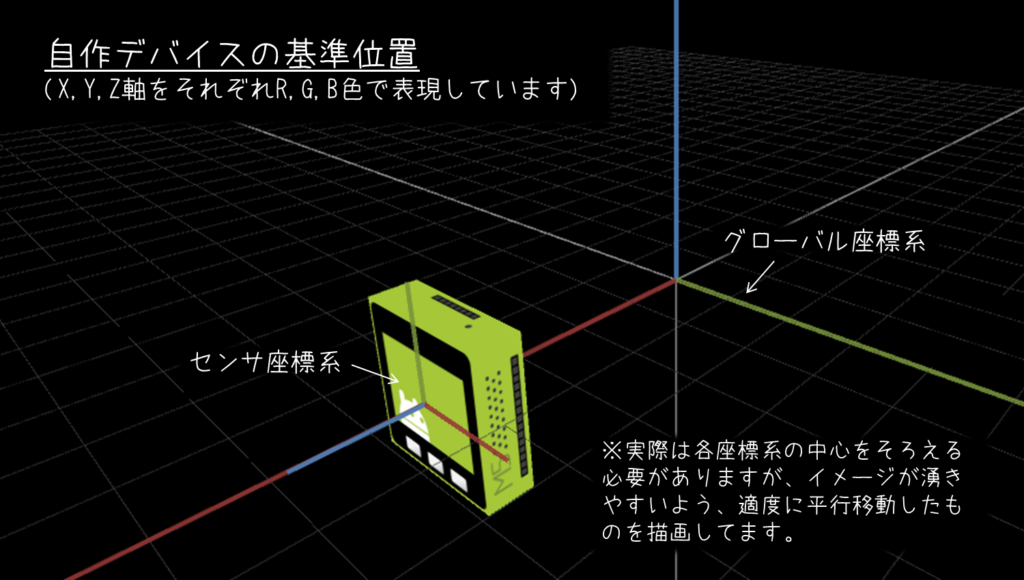
これも毎回出てきますが、自作デバイスでは「グローバル座標系」と「基準姿勢におけるセンサ座標系」の座標軸の向きが揃っていないため、以下のような変換をかませてやります。
座標軸の向きが揃っていない状態における角速度センサの出力(いわばM5Stackの「生」のセンサ値)を \( (w_{x5},w_{y5},w_{z5}) \)、揃えた後のセンサ出力を \( (w_x,w_y,w_z) \) とする場合、先ほどの図における軸の対応関係から、今回必要な変換は次の通り。
\left[
\begin{array}{c} w_x \\ w_y \\ w_z
\end{array} \right]
=
\left[
\begin{array}{c} w_{z5} \\ w_{x5} \\ w_{y5}
\end{array} \right]
$$
角速度センサの弱点
今まで見てきたように、角速度センサを使った姿勢推定では「前回の姿勢」に「最新の回転角」を足しこむ、という事を繰り返します。
このため「誤差が累積する」という、避けようのない特性があります。
その弊害の一つが、動画中盤で登場する「ドリフト」と呼ばれる現象で、センサ値にオフセットが乗ってしまっていることに起因します。
オフセットが乗っていると、実際には静止していてもセンサ出力が0にならないため「まるで回転しているような状態」に見えてしまいます。
その結果、一つ一つは微小な回転であったとしても、それがだんだんと姿勢に蓄積され、時間の経過とともに誤差が大きくなってしまいます。
このため、実物を動かしていないのに、動画のシミュレート結果ではゆら~っと一定方向に動いていってしまっているわけですね。
しかもこのオフセットは結構厄介で、温度など様々な要因で変わったりします。
このオフセットを除去するため、色々な手法が提案されているようですが、今回は静止状態での出力値を覚えておき、それでオフセットをキャンセルする、という単純な方法をとってみました。
おわりに
今回は、角速度センサから姿勢を推定する方法について述べました。
角速度センサは「高周波な(=細かい)動きを検知できる」という強みがある一方、「誤差が累積する」という弱点があります。
このため、この「累積誤差」をリセットするため、今まで勉強してきた「加速度センサ」や「方位センサ」と組み合わせた使われ方をすることが多いです。
このように、お互いの弱点を補うために複数のセンサを使って姿勢を推定する方法を「センサフュージョン」と呼びます。
センサフュージョンとして色々な手法が提案されているのですが、次回はその中の一つをご紹介したいと思います。
では、また次回をお楽しみに(いや~、今回はホント長かったなぁ…)。