逆運動学(IK: Inverse Kinematics)とは、大雑把にいうと「リンクの始点と終点の位置・姿勢を決めた際、その間をうまくつなぐ各リンクの関節角を求める」ことです。

今回は、「体」と「足裏」の位置・姿勢をそれぞれ決めた際、その間の足の各関節角を幾何的に解く方法について解説します。

まずは、イメージを掴むため、IKを適用して動かしてみた動画をご覧ください。

今回の解説の流れは次の通り。
----
・IKの種類
・制約条件
・数学的な基礎知識
・IKの幾何的解法
----

なお、専門ではないので、基本的に疑いの眼差しでご覧頂けると幸いです。

IKの種類

IKは、解析的に解く方法と、数値的に解く方法の２種類があります。

２つを比較した大雑把な特徴は、以下の通り。

今回解説する方法は、解析的な解法の一種になります。

幸いにも、AIさんの足の機構は、特定の条件下において幾何的に解くことができましたので、これを紹介します。

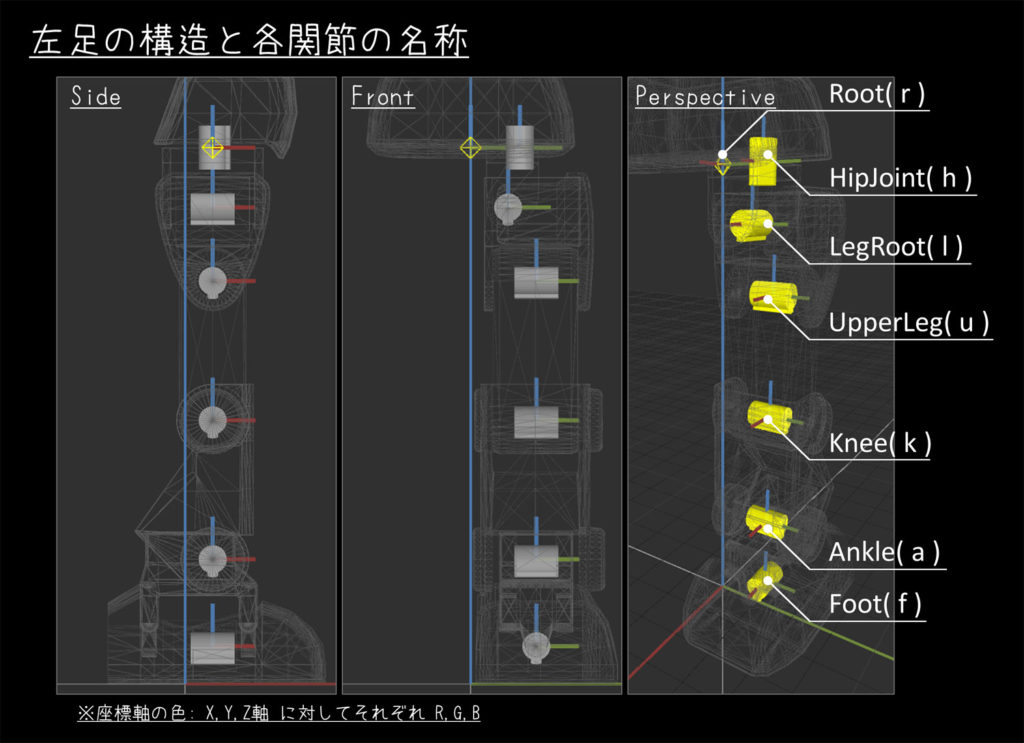
AIさんの足の構造

AIさんの足は左右対称であるため、今回は左足に着目して考えることにします。

座標軸の色は、XYZ軸の順にRGBで示しており、関節の回転軸は円柱で表現しています。
(回転が分かりやすいように、ツマミ付き)

また、Rootがグローバル座標系のZ軸上に来るような配置としています。

各関節のオフセットはX軸方向ですべて揃っており、Y軸方向についてもUpperLeg以降は揃って並んでいます。

この後の理解をスムーズに進めるため、各関節軸がロール・ピッチ・ヨーのどの軸となっているか、把握しておきましょう。

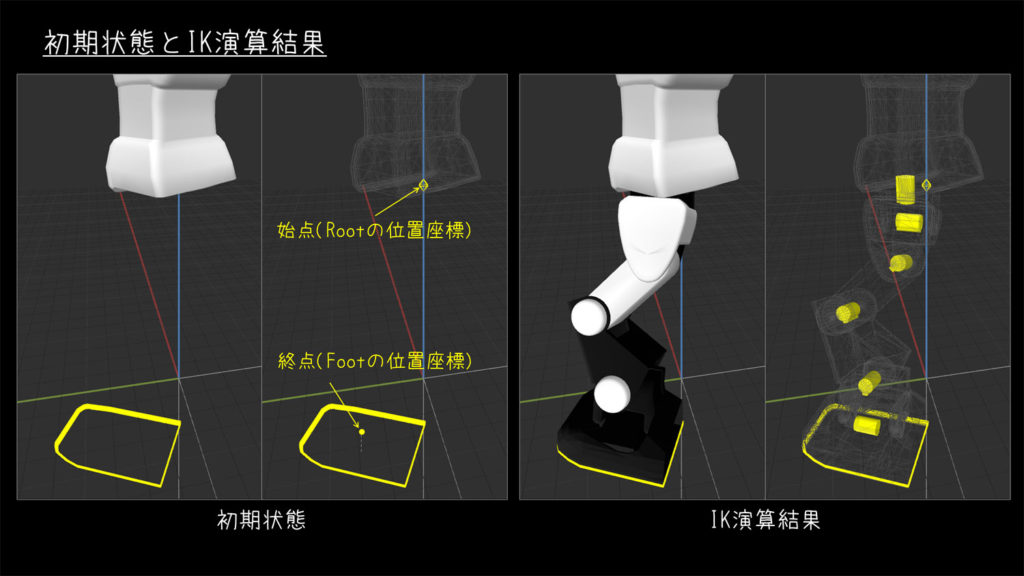
制約条件

今回は幾何的に解くための制約として、次の条件を考えます。

全体像が見えるよう、この制約を満たす一例として、次のような初期状態とその演算結果を示します。

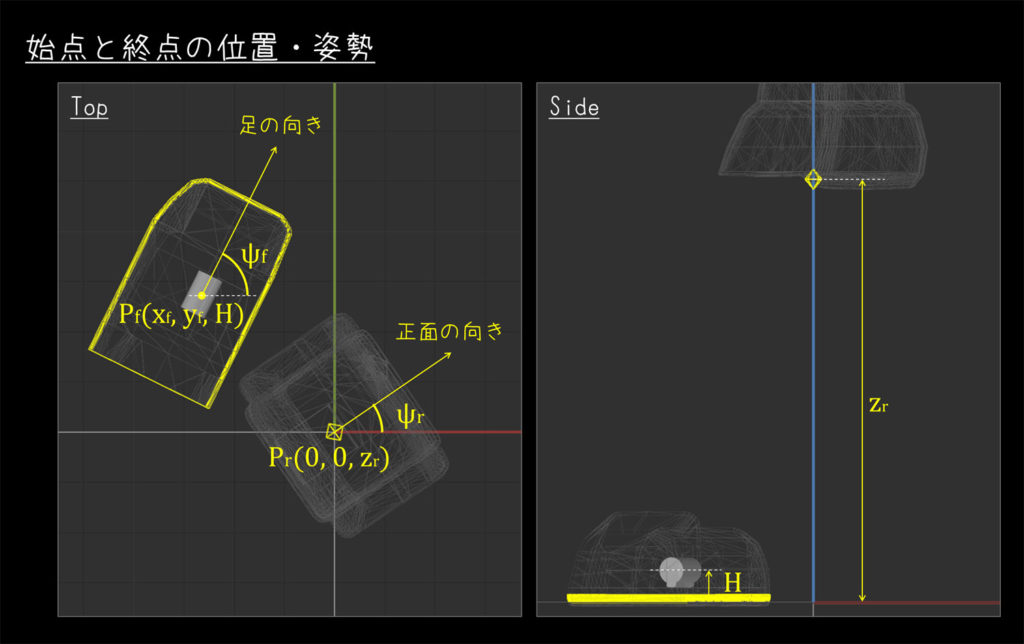
始点・終点について、もう少し数学的に定義しておきます。

位置について、始点(Root)を \( P_r(0,0,z_r) \) 、終点(Foot)を \( P_f(x_f, y_f, {\rm H} ) \) とします。

また、姿勢については制約1,2により、グローバル座標系におけるヨー回転のみ、ぞれぞれ \( \psi_r \) 、 \( \psi_f \) を与えるものとします。

ここで、\( {\rm H} \) はAIさんの靴の高さにより決まる固定値、それ以外の変数はユーザが自由に指定できる値、となります。

IKを解く順番のイメージとしては、始点と終点から、お互いに中央の関節に向かって、じわりじわりと関節角(+位置)を求めていく感じになります。

数学的な基礎知識

IKを幾何的に解く前に、把握しておくべき数学的な基礎知識について解説します。

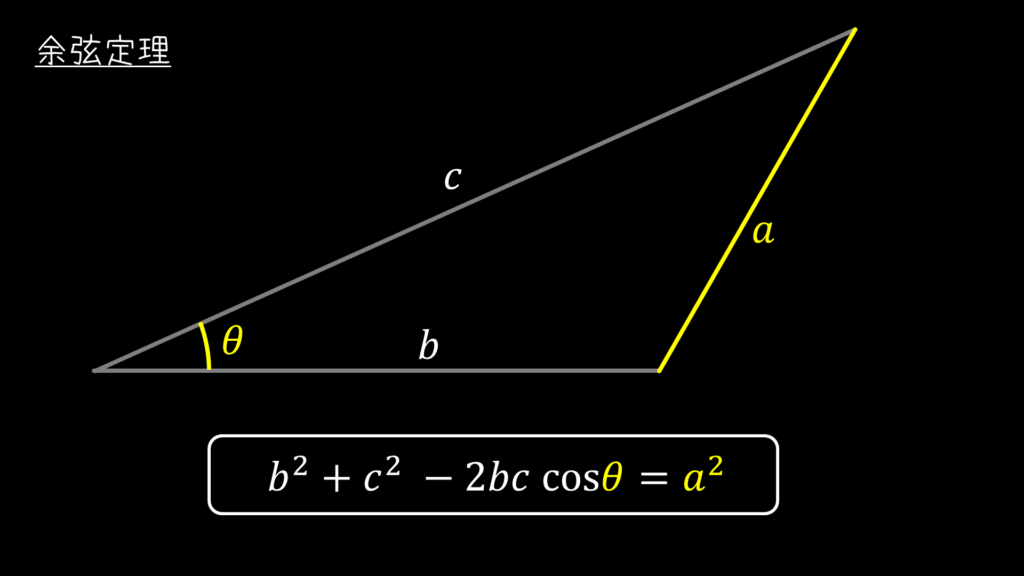
余弦定理

高校で習ったアレです。懐かしや。

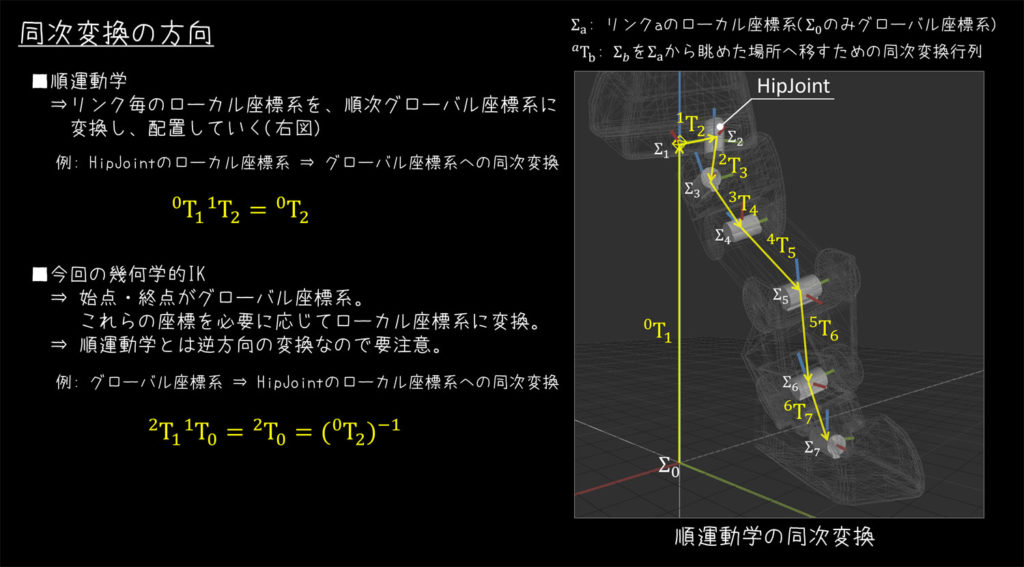
グローバル座標系からローカル座標系への変換

幾何的に関節角を求めるためには、関節軸と直行する平面へ各リンクを投影して考える事になります。

この際、関節軸と直行する平面としてローカル座標系を利用しますが、始点・終点がグローバル座標系であるため、グローバル座標系からローカル座標系への変換が必要となります。

この変換は、普段よく見る順運動学の変換方向とは逆になりますので、簡単に図にまとめてみました。

ここで、回転成分 \( \boldsymbol{R} \) 、平行移動成分 \( \boldsymbol{p} \) を持つ同次変換行列を \( \boldsymbol{T} \) とすると、その逆変換行列 \( \boldsymbol{T}^{-1} \) は次のように表すことができます。
$$
\boldsymbol{T}^{-1} = \left[ \begin{array}{ccc|c}
\\
& \boldsymbol{R}^T & & -\boldsymbol{R}^T \boldsymbol{p} \\
\\
\hline
0 & 0 & 0 & 1
\end{array} \right]
$$

今回の幾何的IKでは、各関節の相対位置が重要になるため、平面への投影の際には回転行列成分だけ求まっていれば十分です。

IKの幾何的解法

では、ここから幾何的に各関節角を求めていくことにします。

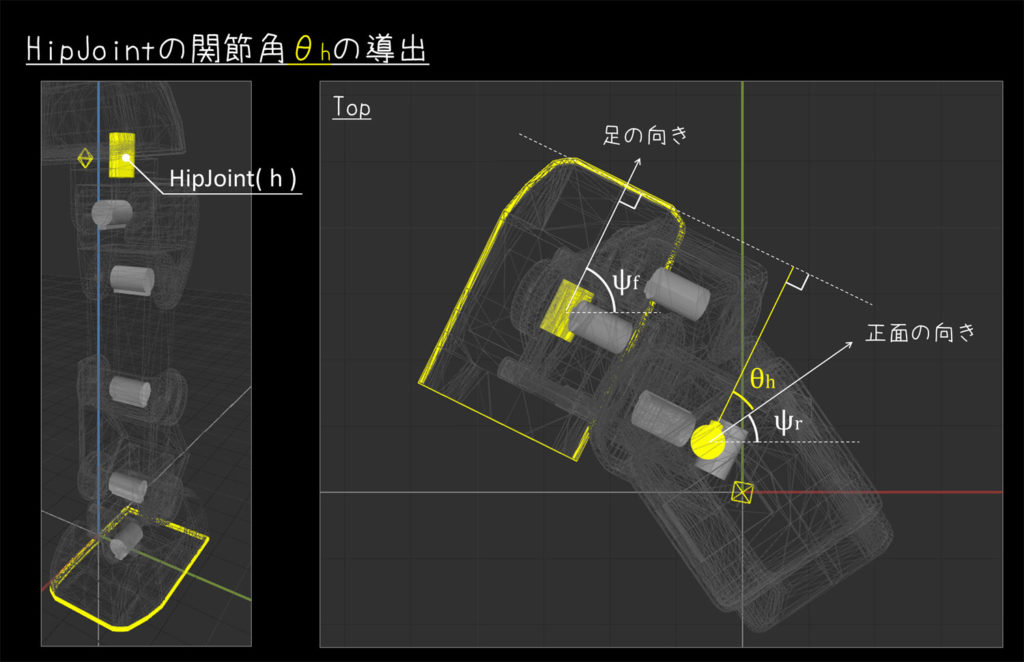
HipJointの関節角

HipJointの回転軸は、制約1により必ずZ軸方向となります。

このため、ちょうど真上から眺めて、XY平面に投影して考えることができます。

また、ヨー軸に対する回転は、足の各関節の中でもHipJointのみであるため、足先の向きにより一意に関節角が求まります。

$$
\theta_h = \psi_f - \psi_r
$$

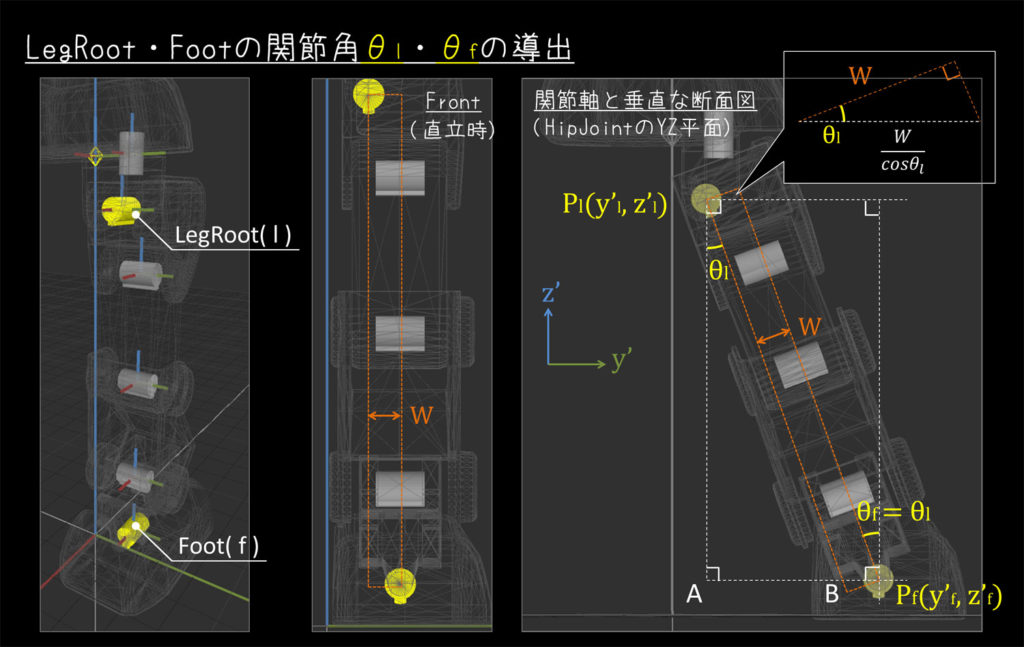
LegRoot・Footの関節角

LegRoot・Footの関節軸と直行する平面として、HipJointのローカル座標系へ投影して考えます。

LegRoot、Footのグローバル座標系における位置について、HipJointのYZ平面へ投影した頂点をそれぞれ \( P_l(y'_l, z'_l) \) 、 \( P_f(y'_f, z'_f) \) としています。
(投影後の値という意味で、ダッシュ(\('\))を付加しています)

また、\( {\rm W} \) は直立時におけるLegRootとFootのY方向のオフセット量で、AIさんの足機構に依存する固定値となります。

ここで、制約1,2より、\( \theta_l = \theta_f \)が成り立ちます。

このため、ここでは \( \theta_l \) を求めることを目標に、解いていくことにします。

まず、\( \triangle ABP_l \) に着目すると、次のような式が成り立ちます。
$$
\tan\theta_l = \frac{AB}{P_lA} = \frac{(y'_f-y'_l)-\frac{\rm W}{\cos\theta_l}}{z'_l - z'_f}
$$

\( a = (y'_f-y'_l) \) 、 \( b = (z'_l - z'_f) \) と置いて少し整理すると
$$
a-b\tan\theta_l = \frac{\rm W}{\cos\theta_l}
$$

両辺を二乗して
$$
\begin{eqnarray}
(a-b\tan\theta_l)^2 &=& \frac{1}{\cos^2\theta_l}{\rm W}^2 \\
\Leftrightarrow a^2-2ab\tan\theta_l+b^2\tan^2\theta_l &=& (\tan^2\theta_l+1){\rm W}^2
\end{eqnarray} \\
\Leftrightarrow (b^2-{\rm W}^2)\tan^2\theta_l -2ab\tan\theta_l +(a^2-{\rm W}^2) = 0
$$

２次方程式の解の公式より

$$
\begin{eqnarray}
\tan\theta_l &=& \frac{2ab \pm \sqrt{ 4a^2b^2 - 4(b^2-{\rm W}^2)(a^2-{\rm W}^2) } }{2(b^2-{\rm W}^2)} \\
&=& \frac{ab \pm {\rm W} \sqrt{ a^2+b^2-{\rm W}^2 }}{b^2-{\rm W}^2}
\end{eqnarray}
$$

ここで、\( \theta_l = 0 \) の時、幾何的に \( a = {\rm W} \) となることを考えると
$$
\tan\theta_l = \frac{ab - {\rm W} \sqrt{ a^2+b^2-{\rm W}^2 }}{b^2-{\rm W}^2}
$$

以上より

$$
\theta_l = \arctan \left( \frac{ab - {\rm W} \sqrt{ a^2+b^2-{\rm W}^2 }}{b^2-{\rm W}^2} \right)
$$

ふー、求まったぜ。

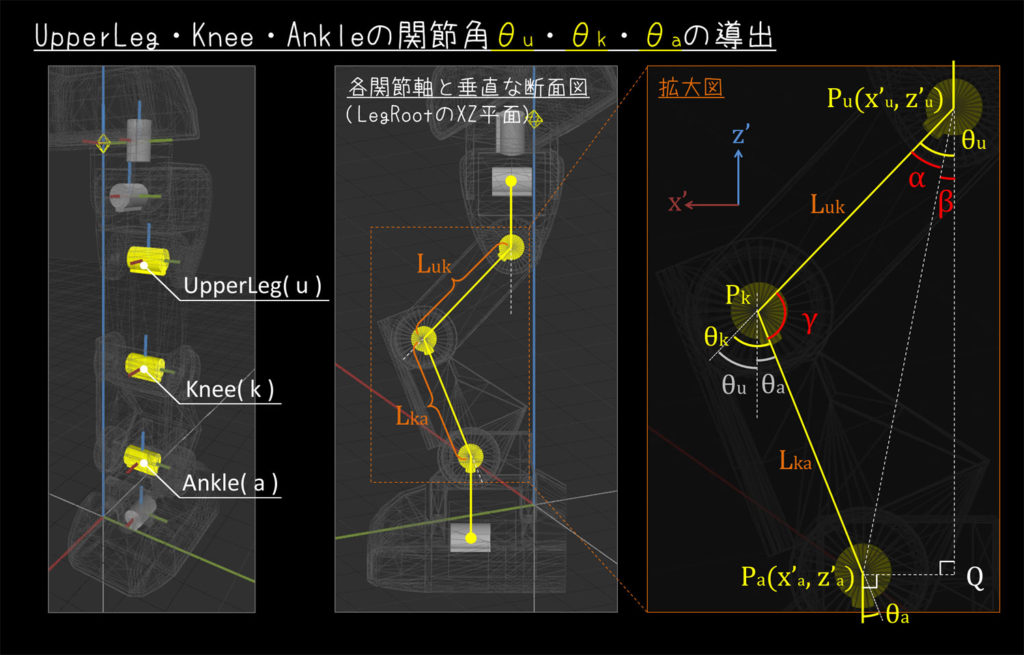
UpperLeg・Knee・Ankleの関節角

UpperLeg・Knee・Ankleの関節軸と直行する平面として、LegRootのローカル座標系へ投影して考えます。

UpperLeg、Ankleのグローバル座標系における位置について、LegRootのXZ平面へ投影した頂点をそれぞれ \( P_u(x'_u, z'_u) \) 、 \( P_a(x'_a, z'_a) \) としています。

また、\( {\rm L_{uk}} \) および \( {\rm L_{ka}} \) は、リンクの長さを示しており、AIさんの足機構に依存する固定値となります。

ここで、制約1,2より、\( \theta_a = \theta_k - \theta_u \)が成り立ちます。

このため、ここでは \( \theta_k \) と \( \theta_u \) を求めることを目標に、解いていくことにします。

まず初めに、\( P_u P_a \) の長さ \(L_{ua}\) を求めておきます。
$$
L_{ua} = \sqrt{ (x'_a-x'_u)^2 + (z'_a-z'_u)^2 }
$$

次に、\( \triangle P_uP_kP_a \) において、\(\gamma\) に着目した余弦定理により、次の式が導出されます。
$$
\begin{eqnarray}
L_{ua}^2 &=& {\rm L_{uk}^2+L_{ka}^2-2L_{uk}L_{ka}}\cos\gamma \\
\Leftrightarrow \cos\gamma &=& \frac{{\rm L_{uk}^2+L_{ka}^2}-L_{ua}^2}{\rm 2L_{uk}L_{ka}} \\
\Leftrightarrow \gamma &=& \arccos\left(\frac{{\rm L_{uk}^2+L_{ka}^2}-L_{ua}^2}{\rm 2 L_{uk}L_{ka}}\right)
\end{eqnarray}
$$

以上より、\( \theta_k \) が求まります。
$$
\begin{eqnarray}
\theta_k &=& \pi - \gamma \\
&=& \pi - \arccos\left(\frac{{\rm L_{uk}^2+L_{ka}^2}-L_{ua}^2}{\rm 2L_{uk}L_{ka}}\right)
\end{eqnarray}
$$

次に、\( \triangle P_uP_kP_a \) において、\(\alpha\) に着目した余弦定理により、次の式が導出されます。
$$
\begin{eqnarray}
{\rm L_{ka}}^2 &=& {\rm L_{uk}^2}+L_{ua}^2-2{\rm L_{uk}}L_{ua}\cos\alpha \\
\Leftrightarrow \cos\alpha &=& \frac{{\rm L_{uk}^2}+L_{ua}^2-{\rm L_{ka}^2}}{{\rm 2L_{uk}}L_{ua}} \\
\Leftrightarrow \alpha &=& \arccos\left(\frac{{\rm L_{uk}^2}+L_{ua}^2-{\rm L_{ka}^2}}{{\rm 2L_{uk}}L_{ua}}\right)
\end{eqnarray}
$$

また、\( \triangle P_uP_aQ \) に着目すると
$$
\begin{eqnarray}
\tan\beta &=& \frac{P_uQ}{QP_a} \\
&=& \frac{z'_u-z'_a}{x'_a-x'_u}　　　　　※座標軸の向きから、uとaの順番に注意 \\
\Leftrightarrow \beta &=& \arctan\left(\frac{z'_u-z'_a}{x'_a-x'_u}\right)
\end{eqnarray}
$$

以上より、\( \theta_u \) が求まります。
$$
\begin{eqnarray}
\theta_u &=& \alpha + \beta \\
&=& \arccos\left(\frac{{\rm L_{uk}^2}+L_{ua}^2-{\rm L_{ka}^2}}{{\rm 2L_{uk}}L_{ua}}\right) + \arctan\left(\frac{z'_u-z'_a}{x'_a-x'_u}\right)
\end{eqnarray}
$$

おわりに

いやー、記事を書くの大変でした…。(特に図を用意する所。専用で実装したゾ)

しかし、振り返って再度まとめる事で、変なバグを発見したり、今までモヤモヤしていた部分がスッキリしたので、頑張った甲斐がありました。

今回の幾何的なIKは、ヤコビアンの逆行列を使ったIK時に発生する特異姿勢(足を完全に伸ばした時など)のようなものが無い(はず？)ので、その点のメリットも大きいかと思います。(追記: ただし、昔と違って今は数値的な解法でも特異姿勢関係なく解けるらしいです)

いや、そもそも幾何的なIKでも、もしかしたら三角関数の逆変換時の精度が問題になるケースがあるかも？と、色々と勉強不足な部分があるので、突っ込みがあればぜひご教授ください。

ということで、今回はAIさんの足のIKを、一定の制約下で幾何的に解いてみるお話でした。

記事の中でも登場したように、今後、かかと・つま先のみ接地の場合のIKも解説してみようと思っています。

ということで、また次回をお楽しみに。